16. 文本:线性模型假设
模型假设及相应的解决方法
之前的视频曾提到 统计学习简介 一书,其中就提到了如下五个假设:
- 因变量-自变量关系的非线性
- 误差项的相关性
- 非恒定方差和正态分布误差
- 异常值/高杠杆点
- 共线性
本文总结了判断上述问题是否存在的方法以及相应的解决办法。这是统计学家面试时经常提出的问题,但该问题是否有实际意义取决于你创建模型的目的。在接下来的概念中,我们会更仔细地研究某些相关知识点,因为我觉得我们需要额外注意那些,但下方为你列出了各知识点的详尽介绍,我们先来仔细看看下文涉及的每一项。
线性
线性是假设因变量和自变量之间真的存在可用线性模型解释的关系。如果线性假设不为真,那你的预测结果就不会很准确,此外,与系数有关的线性关系也就没什么用了。
为了评估某段线性关系是否合理,一个很实用的方法是做预测值 (\hat{y}) 的残差 (y - \hat{y}) 图。如果图中出现多个曲线部分,那就意味着线性模型实际上可能并不拟合数据,自变量和因变量存在其它关系。创建非线性模型的办法有很多(甚至可以线性模型的形式来创建),其中几种办法会在本课后面的内容中提及。
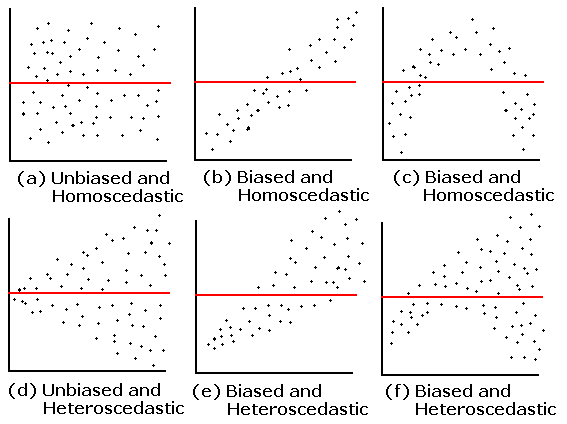
在本页底部的图片里,这些称为 偏差 模型。理想来说,我们想要的是像图片左上角残差图那样的随机散点图。
相关误差
如果我们是随时间变化来收集的数据(比如预测未来股价或利率),或数据与空间有关(如预测洪涝或干旱地区),那就很容易出现相关误差。通常,我们可以用过去数据点提供的信息(针对与时间有关的数据)或用相邻数据点提供的信息(针对与空间有关的数据)来提高预测结果。
不考虑相关误差的主要问题在于:往往你会利用这一相关性,得到更好的未来事件预测数据或空间关联事件预测数据。
要判断是否有相关误差,最常用的方法是观察收集数据的域。要是你不确定的话,你可以试试一个叫 Durbin-Watson 的检验方法,人们常用该测试来评估误差相关性是否造成问题。还有 ARIMA 或 ARMA 模型,人们常用这两个模型来利用误差相关性,以便做出更佳预测。
非恒定方差和正态分布误差
你预测的值不同,得到的预测值范围也不同,那就意味着方差不恒定。非恒定方差对预测好坏影响不大,但会导致置信区间和 p 值不准确,这种时候,在预测值接近实际值的那部分区域,系数的置信区间会太泛,而在预测值较远离实际值的区域则会太窄。
通常来说,对数函数(或使用其它反应变量的变换方式)能够 “摆脱” 非恒定方差,而要选择合适的变换方式,我们一般会用 Box-Cox 。
用预测值的残差图也可以评估非恒定方差。在本页底部的图片中,非恒定方差的标签为 异方差 。理想来说,我们要的是一个有异方差残差的无偏模型(其异方差残差在一定数值范围内保持不变)。
虽然本文并不探讨残差的正态性,如果你想创建可靠的置信区间,正态性回归假设就十分重要了,更多相关信息详见 这里 。
异常值/杠杆点
异常值和杠杆点是远离数据正常趋势的点。这些点会对你的解造成很大的影响,在现实中,这些点甚至可能是错误的。如果从不同来源收集数据,你就可能在记录或收集过程中造成某些数据值出错。
异常值也可能是准确真实的数据点,而不一定是测量或数据输入错误。在这种情况下,'修复'就会变得更为主观。要如何处理这些异常值往往取决于你的分析目的。线性模型,特别是使用最小二乘法的线性模型,比较容易受到影响,也就是说,大异常值可能会大幅度地左右我们的结果。当然,异常值也有一些解决技巧,也就是我们常说的 正则化 。本课不会谈及这些技巧,但在 机器学习纳米学位免费课程 中,我们对这些技巧做了粗略的介绍。
而在宾夕法尼亚州立大学提供的完整回归课程里,就有特别长的篇幅在探讨杠杆点的问题,详见 这里 。
共线性(多重共线性)
如果我们的自变量彼此相关,就会出现多重共线性。多重共线性的一个主要问题在于:它会导致简单线性回归系数偏离我们想要的方向。
要判断是否有多重共线性,最常见的办法是借助二变量图或 方差膨胀因子 (即 VIFs) 。下一概念我们就要更深入地探讨多重共线性,因而在此不做赘述。